5360. Астрономия
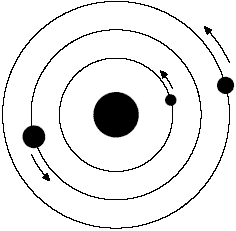
Вокруг звезды вращается n планет. Тангенциальная скорость планет
постоянна. Направление вращений планет одинаково. Парадом планет называется
момент времени, в который все планеты располагаются на одной прямой. Необходимо
вычислить промежуток времени между последовательными парадами планет.
Вход. Первая
строка содержит количество планет n
(2 £ n £ 1000). Вторая строка содержит n
чисел – периоды вращения планет ti
(1 £ ti £ 10000). Не все ti
одинаковы.
Выход. Вывести время между последовательными
парадами планет в виде несократимой дроби, разделяя числитель и знаменатель
пробелом.
Пример входа
3
2 6 3
Пример выхода
3 1
РЕШЕНИЕ
НОД, НОК
Анализ алгоритма
Обозначим
через t искомое минимальное время
между последовательными парадами планет. Частное t / ti представляет собой часть круга, которую i-ая планета пройдет за время t. Рассмотрим i - ую и j - ую планету с периодами вращения соответственно
ti и tj. Они вместе с солнцем будут находиться на одной прямой
через время t, если
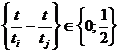
Здесь
через {x} обозначена дробная часть
числа x. То есть разница t / ti – t / tj будет представлять собой либо
целое число кругов, либо целое с половиною.
Или
то же самое, что значение
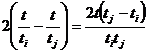
является
целым. Поскольку i и j – любые значения от 1 до n, а значение t = a / b требуется вывести в виде несократимой
дроби, то значения a и b следует выбрать так чтобы:
·
a было минимально возможным и
делилось на все значения t1,
t2, .., tn.
·
b было максимально возможным и
делилось на два и на все возможные разницы ti
–tj.
то
можно утверждать, что число
K = 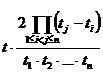
должно
быть целым. Если в качестве t взять
значение a / b, где
a = НОК(t1, t2,
…, tn), b = 2 * НОД(t1 – t0,
t2 – t0, …, tn
– t0),
то
значение K будет целым. Переменной t0
следует присвоить наименьшее значение из ti.
Осталось сократить дробь a / b на их наибольший общий делитель.
Покажем,
как вычислить a = НОК(t1, t2, …, tn),
совершив минимум операций над большими числами (значение а является большим). Переберем все пары (ti, tj),
i < j , для каждой пары вычислим d =
НОД(ti, tj), после чего разделим tj на d. После этого произведение оставшихся ti равно значению а.
Пример
Рассмотрим
пример, приведенный в условии задачи. Для его данных имеем:
a = НОК(2, 6, 3) = 6,
b = 2 * НОД(6 – 2, 6 – 3) = 2 *
НОД(4, 3) = 2
Откуда
искомый ответ в виде несократимой дроби имеет вид: a / b = 3 / 1.
Рассмотрим
процесс вычисления a = НОК(2, 6, 3).
После описанного двойного цикла перебора всех пар (ti, tj)
и сокращения tj на d массив t будет содержать числа (2, 3, 1). Их произведение равно 6.
Реализация алгоритма
Читаем
входные данные.
scanf("%d",&n);
for(i = 0; i < n; i++)
scanf("%d",&t[i]);
Совершим частичную сортировку массива t так, чтобы в t[0]
находился минимальный элемент.
partial_sort(t,t+1,t+n);
В переменной _gcd вычисляем выражение 2 * НОД(t1 – t0,
t2 – t0, …, tn
– t0).
_gcd = t[1] -
t[0];
for(i = 2; i < n; i++)
_gcd = gcd(_gcd,t[i] - t[0]);
_gcd *= 2;
После выполнения следующего двойного цикла НОК(t0, t1, t2,...,
tn) = t0 * t1
* t2 * ... * tn.
for(i = 0; i < n; i++)
for(j = i+1; j < n; j++)
{
d = gcd(t[i],t[j]);
t[j] /= d;
}
Время
между последовательными парадами планет t
равно a / b, где
a = НОК(t1, t2,
…, tn), b = 2 * НОД(t1 – t0,
t2 – t0, …, tn
– t0),
Остается разделить произведение t0 * t1
* t2 * ... * tn на _gcd. В следующем цикле
попробуем сократить _gcd с каждым из значений ti.
for(i = 0; i < n; i++)
{
d =
gcd(t[i],_gcd);
t[i] /= d; _gcd /= d;
}
Вычисляем произведение чисел в массиве t при помощи
длинной арифметики и выводим ответ в виде дроби.
a =
BigInteger(t[0]);
for(i = 1; i < n; i++)
a = a * t[i];
a.print();printf(" %d\n",_gcd);
2
2 4
ответ
2 1
Нок = 4
Нод = 2
4 12 20
15/4 = 3¾
15/12 = 5/4 = 1 ¼
15/20 = ¾
А = Нок = 20*3 =60
Б = нод(8, 8) = 8
2 (12-4) 2*8 1
- - - -- - - = ----- = ----
4 * 12 2*8*3 3
2 (20 - 12) 2*8 1
- - - -- - - = ----- = ----
12 * 20 3*5*16 15
2 (20 - 4)
2*16 2
- - - -- - - = ----- = ----
4 * 20 5*16 15
ответ
15 1